問題描述:
直接積分法的時程分析采用的瑞利阻尼有什么含義�����,該如何指定��?
解答:
瑞利阻尼(Rayleigh)是目前地震響應分析中最常采用的阻尼模型之一���,在 SAP2000 和 ETABS 中采用直接積分法做時程分析時,可以直接通過瑞利阻尼定義結構的阻尼大小���。
瑞利阻尼由兩部分構成:一項與質(zhì)量矩陣成正比�,一項與剛度矩陣成正比,其表達式為:

其中:[CM]=α0[M]�����,[CK]=α1[K]�。相應地,阻尼比也分為兩項組成:與質(zhì)量矩陣成正比項和與剛度矩陣成正比項����,

其中:ξM=α0/2ωn,ξM=α1ωn/2
確定兩個頻率點 ωi 和 ωj 及其對應的阻尼比 ξi 和 ξj 就可以求解瑞利阻尼的比例系數(shù) α0 和 α1��。給定比例系數(shù) α0 和 α1 后�����,可以看到阻尼 ξM 和 ξK 僅與 ωn 有關��。下圖給出了阻尼比隨頻率的變化規(guī)律曲線�。
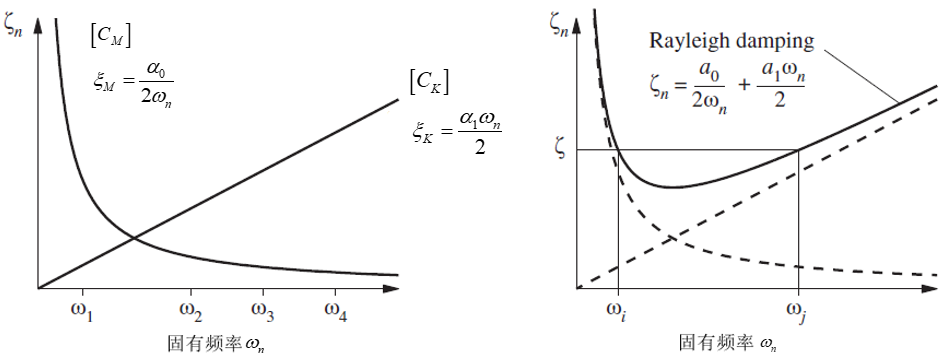
由上圖可知��,當結構頻率趨近于 0 時����,與質(zhì)量相關的阻尼值 ξM 將會變得無窮大��,而與剛度相關的阻尼 ξK 接近于0����。質(zhì)量阻尼 ξM 隨著頻率的增加而迅速變小�����,剛度阻尼 ξK 則與頻率成正比���,則隨著頻率的增加而線性增加���。當頻率趨近于無窮大時,剛度阻尼 ξK 同時趨近于無窮大����,而質(zhì)量阻尼 ξM 則趨近于無窮小。
在定義瑞利(Rayleigh)阻尼時����,不能隨意選取頻率點 ωi 及其對應的阻尼比確定比例系數(shù)。當結構的振動頻率在區(qū)間 [ωi�����,ωj] 之內(nèi)時,結構的阻尼比將略小于給定阻尼比���,結構的反應將略大于實際的反應��,這樣的計算結果對工程而言是安全的�����。而當頻率在 [ωi����,ωj] 區(qū)間之外時��,其阻尼比均大于給定阻尼比���,而且距離該區(qū)間越遠,阻尼比越大���。區(qū)間頻率之外的振動反應會被抑制�,其計算值將遠遠小于實際值��。通常來說區(qū)間頻率之外一部分是不需要考慮的,或可以忽略的�,但是,如果存在對結構設計有重要影響的頻率分量���,則可能導致嚴重的不安全���。
依據(jù) CSI 的建議,瑞利阻尼可以通過指定結構的周期來定義���。其中����,第一周期可以取為 0.9T1�����,第二周期取 0.2T1(取 0.9T1 而非 T1 是為了防止阻尼偏小過多)�����。另外����,也有建議第一周期取相應地震方向的第一階周期�,第二周期取質(zhì)量參與系數(shù)達到 90% 時的振型周期
����,這樣算出來位移會偏大,因為阻尼比普遍偏小��。對于這兩個周期(或頻率)的取值��,用戶應謹慎填寫����。必要的情況下,應調(diào)整周期的取值�����,查看結構的響應對其是否敏感��。